Pythagoras - 'all is number'
This web page is quoted from the author's book Principles of nature; towards a new visual language, WA Roberts P/L Canberra. 2003. [Used with permission of the author] includes some minor editing and reformatting for the web.
Science historian Brian Silver said, ‘Pythagoras, more than anyone else, has the right to be considered the father of the Western way of seeking order in the universe. His influence stretches from ancient Greece to the modern world.’ (BL Silver, 1998, p. 174). Born about 580 B.C., not a shred of Pythagoras’ writing remains, and yet his name seems to be virtually inscribed in the psyche of so many cultures ever since, primarily (and almost exclusively in our own time) associated with the eponymous theorem concerning the square on the hypotenuse . But his legacy is far weightier than that of the famed theorem. His statue stands ‘alongside that of Aristotle, Euclid, Ptolemy, and Christ…above the massive west door of Chartres cathedral’ (BL Silver, 1998, p. 170). Even in the remote antipodean outpost, Australia, his name appears, carved in stone, high on the northern wall of Sydney’s major public art museum, the Art Gallery of New South Wales.
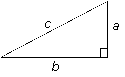
Figure 3 Pythagoras ’ Theorem states that in any right triangle , of legs a and b and hypotenuse c, that, a2 + b2 = c2 |
That the Pythagoreans were obsessed with number is unquestionable. But the obsession was not baseless. Too many ‘coincidences’, too many connections—between number and number, number and shape, number and music—led them to re-examine the accepted world view of their day. Numbers, as originally conceived, were the pragmatic progeny of accounting and commerce; but slowly, as they ‘grew’, were seen by the Pythagoreans (and others) as having a meaning that stretched far beyond the mere representation of ‘quantities’ and the collections of material objects that had spawned their introduction. Again, Silver indicates how the Pythagorean vision marked a fundamental turning point in the attitude not only to numbers, but indeed to nature itself,
The Pythagoreans appear to be the first to have stated that mathematics was an activity that could be divorced from the practical world. Mathematics undoubtedly arose from practical needs such as commerce and the construction of buildings. It was the Pythagoreans who saw that there was an abstract entity behind the socially useful instrument. This was one of the critical turns, if not the critical turn, in the history of mathematics, and it had a deep influence on later Greek thinkers, Plato and Euclid in particular. It is here that we see the beginning of what is today called basic science, the study of nature, and knowledge, for its own sake. Plato, a firm Pythagorean, specifically stated that arithmetic should be studied for its intrinsic value, not for the purposes of commerce. |
|
This distinction between the pragmatic and abstract consideration of numbers became formally acknowledged in Greek language and culture. Wells states (D Wells, 1997, p. 61),
The Greeks distinguished between logistike (whence our term logistics), which meant numeration and computation, and arithmetike, which was the theory of numbers themselves. It was arithmetike that Plato, a convinced Pythagorean, insisted should be learned by every citizen of his ideal Republic, as a form of moral instruction.
To the Pythagoreans arithmetike gave form to music, and music to form. Patterns appeared—and the Pythagoreans seemed to know where to look. They sought to map out the grammar of a language that spoke even of itself, but in numbers rather than in words. Whereas for many of their compatriots, numbers were merely ‘subjects’ within the laws of commerce, for the Pythagoreans, the whole cosmos seemed subject to the law of number.
The Pythagorean Theorem
The following is quoted from my book (W. Roberts, 2003, pp.116-—117) with some minor editing and reformatting for the web.
[Pythagoras' Theorem is] one of the most fundamental theorems (if not the most fundamental) in all of mathematics. It concerns, oddly enough, a certain class of triangle, the ‘right triangle ’ in which one angle equals ninety degrees also known as a right angle.
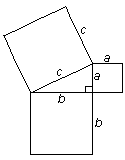
...Expressed geometrically, [it states that, in a triangle in which one angle equals a right angle] the area of the square constructed on the hypotenuse (which equals c2) is equal to the sum of the areas of the squares constructed on the other two sides (that is a2 + b2)...
After more than two thousand years, and in an age dominated by microchips and electronic number-crunching at unthinkable speeds, Pythagoras' Theorem remains as one of the most profound in all of mathematics. So much mathematics since has drawn upon it, built upon it, that were it to be removed, virtually the entire edifice of mathematics would be forever changed. It is a theorem that appeals to purist and pragmatist alike, linking geometry and number theory, lengths and areas, especially within the framework of Cartesian (orthogonal) coordinate axes. It is fundamental to vector analysis, and as such, has found application in twentieth century physics such as Quantum Electrodynamics (QED) and the Theory of Special Relativity. It undergirds the trigonometric functions which in turn, relate to more mathematics and science than bears mentioning.
Pythagoras (c.580 - c.480 BC ) and his followers concluded after a string of fascinating discoveries that 'all is number'. The passage of more than two millennia has done nothing to diminish the idea that the Universe is profoundly and fundamentally connected to numbers and the abstract mathematical edifice that surrounds them. In fact, the history of science has revealed a story of unfolding interconnectedness on an awesome scale, and this relationship of things to other things, and of events to other events, is largely mathematical.
The story surrounding Pythagoras is steeped in legend: none of his writings is known to have survived the ravages of two and a half millennia. But it is proof to the depth of his knowledge and influence that, not withstanding the tides of history, his ideas have been handed on down through the generations. Considering the AD 389 and AD 642 desolating conquests of Alexandria , then intellectual capital of the western world, together with the ordered burning of centuries-old manuscripts and books, and, given the intolerance and obscurantism of the ensuing Dark Ages , and still later, the 1453 invasion of Constantinople (which was where most of the surviving manuscripts of past centuries had by this time amassed), . . . it is incredible that we, in the twentieth century, are in possession of any textual legacy at all from the Classical era.
It is a tribute to the farsightedness and courage of many individuals through such stormy times that we are today able to peer back and piece together a picture of Classical Greek knowledge and reasoning. At the time of the Barbarian occupation of the Italian peninsula , one such figure was, Anicius Manlius Torquatus Severimus Boethius . In the words of science historian, Brian Silver (BL Silver, 1998, p. 175),
...he was dubbed A the last of the Ancients. @ It was he who would carry the Pythagorean torch, almost alone, through the millennium that led to the Renaissance.
Boethius' (unrealized) ambition was to translate all the works of Plato and Aristotle into Latin. Pythagoras left no writings; much of what we know of him is contained in Plato's writings, particularly Timaeus. Through Plato, Boethius met Pythagoras.
The translations of Boethius had an enormous influence on medieval learning.
Boethius' books were standard texts in the first universities of twelfth-century Europe. The ideology of music espoused within these books was Pythagorean in its roots, based as it was, on whole-number ratios, which were found to produce harmonious 'intervals' of sound from a vibrating string.
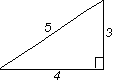
Although the relationship between the hypotenuse and sides of certain right-triangles (e.g. the 3-4-5 triangle...) was apparently known well before the time of Pythagoras, it seems that Pythagoras and his followers were perhaps, in addition to proving it for all right-triangles, among the first to find a general method of generating ‘triples of whole numbers’ which could form the two sides (legs) and hypotenuse of a right-triangle. This is one of the reasons the theorem has been attributed to Pythagoras. These triplets of whole numbers that could form the sides of a right-angle triangle became known as Pythagorean Triads or Pythagorean Triples. The most famous of them is the ‘3-4-5 triad’ as geometrically depicted [in the accompanying figure]. The Pythagoreans and their contemporaries proved that there were an infinite number of such triads.
These findings, together with discoveries in music of a connection between whole-number ratios and ‘harmonious intervals’, no doubt led the Pythagoreans towards their famous proposition that “all is number”.
| back to top |
next > |