Relating units to wholes
Euclidean geometry concerns the geometry of the flat plane. This represents an infinite whole which has interesting and specific properties of division as outlined by Euclid and others. It is known that the regular division of the plane (division of the plane into regular polygons without gaps) is possible in only several ways (see figure 6.2). These possibilities together constitute a resonant scale-structure (in the musical sense of scale).
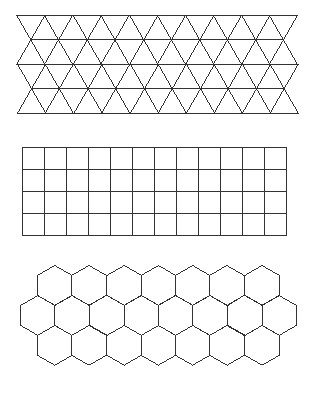 |
If we now ask which of the irregular polygons can tile the plane without gaps, then this scale can be extended to include any triangle, any quadrilateral, and certain irregular hexagons as determined by Escher, (see figure 6.3). Other non-Euclidean geometries (i.e. relating to curved surfaces) have other scale-structures corresponding to the regular divisions of their wholes. These divisions of the plane create units of identical shape and area which fit together without gaps and these shapes are all therefore apt to be employed as units-of-area.
 |
Is it not curious then, that in the history of mathematics, squares have served the role of 'general-purpose units-of-area', it would appear by default rather than design*? We have applied square plugs to nearly every shaped hole under the mathematical sun. The notion of units-relative-to-wholes has not been taken up seriously perhaps for the ironic reason that when seeking to compare the areas of closed planar shapes, we have felt the need for an absolute unit as a universal arbiter of comparison ('this area is so-many-square units whereas that area is a lesser number of equivalent square units, and is therefore smaller'). It is ironic because comparisons involve relating something to something else, and thus a choice of units relative to the system concerned must ultimately be simpler and more powerful.
| We have applied ‘square plugs’
to nearly every shaped hole under
the mathematical sun. |
|
As will be shown in the following pages, the application of relative units to mathematical and spatial problems allows a deeper understanding of qualitative differences as well as a simpler and more resonant connection of geometric problems to number theory and analysis.
| back
to top |
next > |