2 3
The representation of numbers - notation
- early methods of recording numbers were cumbersome and impractical
- efficiency in representing numbers improved when it was realised a single symbol could be used to represent intermediate numbers. These were then variously combined to represent larger numbers (eg groups of tally marks)
- the invention of new symbols (eg the Roman numerals) for a range of intermediate values allowed for the economical recording of significantly larger numbers.
- further developments saw more syntactical ways of combining numerals such as the rules which governed the value of groups of numerals in Roman notation. The advantage of this was that additive and subtractive rules (depending on whether a numeral came before or after another numeral) allowed for large numbers to be represented with even fewer numerals
- a major development came with the introduction of fully positional systems. In these a numeral acquired a second meaning which derived from its position (or column) within a number, and which acted as a multiplier of the numeral's face-value. For example in our base ten number system , the numeral "3" in the number "300" represented 100 multiplied by 3.
The discovery of an efficient method for writing or representing numbers
was a critical development in the history of mathematics. Even the simplest
of patterns among numbers had until then remained largely hidden, obscured
by an often cumbersome or inconsistent system of numerical notation.
For example, although the Roman system of representing numbers possessed
a syntax which determined the reading of numerals within a sequence, this
resulted in numbers whose component numerals bore no consistent positional
meaning from one number to the next but instead obtained their meaning
locally -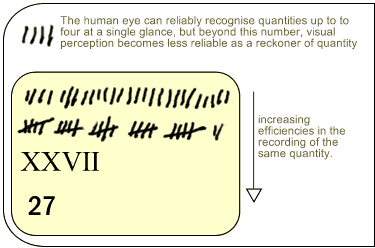 
according
to the adjacent numerals within a given number. This meant that although
numbers could be organised into rows and columns of numerals,
there was no consistent positional meaning of a numeral in a given column
from number to number. A special device (abacus) was invented
in order to achieve speedy operations (such as addition and multiplication)
between numbers, and it is interesting that the abacus which itself possessed
a columnar logic did not quickly 'straighten out' the columnar inconsistencies
of the Roman notation it served.
With many of these early number systems, operations which should have been simple (such as addition and multiplication) were unnecessarily difficult. The difficulties stemmed from the fact that they did not have a place-value system; the notation and its organisation had no intrinsic logic or resonant scale structure. Nor did many of them have a symbol for a null quantity, the zero.
The combined innovations of, firstly, unique symbols for the integral divisions of a base (for example, in base 10, nine numerals were necessary) , secondly, a consistent place-value or positional system in which each column represented incremental powers of the base (eg units, tens, hundreds, etc), and thirdly, the adoption of a symbol for zero, were first harmoniously combined within a system of numerical notation in subcontinental India. This system supplanted virtually every other competitor it met and is more or less the system of notation used to this day.
These combined innovations resounded like harmonics on a vibrating string. The number notation came of age and opened a door to a new and fascinating abstract world of number we now know as mathematics. It was a closing of the circle. This new way of writing numbers contained an inner logic which enigmatically reflected relationships on earth and in the heavens. Ultimately this logic would enable humankind to predict the motions of planets, to measure time, and navigate space. John Barrow sums up the eventual breakthrough in the history of math this way,
. . . something strange happened. These symbols were found to have a life of their own that dictated how they should be manipulated. And the ways in which they were used enabled new facts about the world to be predicted.2
He goes on to note that the move to abstraction in mathematics (the concept of 'number' detached from 'numbers of things'), occurred when the method for recording numbers (the notation) reached a certain threshold of logical organisation itself.
 |
|
| . . . something strange happened. These symbols
were found to have a life of their own that dictated how they should
be manipulated. And the ways in which they were used enabled new facts
about the world to be predicted. |
|
|
|
| back to top |
next > |