The Eutrigon theorem for a new class of Euclidean triangle

Principles of Nature: towards a new visual language

The Eutrigon Theorem - a new* twin to the theorem of Pythagoras

This web page is reproduced from the author's book Principles of nature; towards a new visual language, WA Roberts P/L Canberra. 2003. [Used with permission of the author] Edited and reformatted for the web, including animated diagrams and additional commentary by the author.

Introduction

Scale structure theory has implications not only to the units and measurement of areas but also to triangle classification as we have seen. Particularly pertinent to the theorem presented here on this page is the implementation of the equitriangular unit of area (etu) as we defined earlier. We will also later use our new knowledge of the area of a eutrigon (in terms of these relative units of area, etu) in the algebraic interpretation of the geometric construction (figure ET2) below — a form of resonant scale structure (in the terminology of the new theory) — that visually proves the theorem.

the Eutrigon Theorem

—Geometric Form

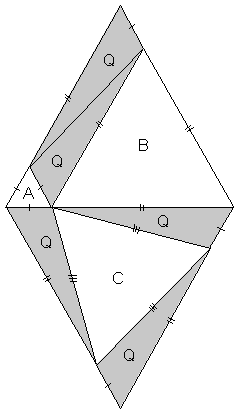
The area of any eutrigon (shaded in figure ET1) is equal to the sum of the areas of the equilateral triangles on its legs a and b, minus the area of the equilateral triangle on its hypotenuse, c.

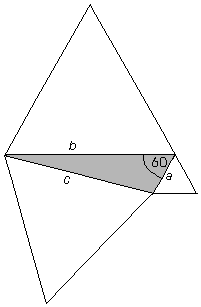
Eutrigon, with equilateral triangles erected on all sides
Figure ET1


Geometric form of Eutrigon Theorem The area of any eutrigon is equal to the sum of the areas of the equilateral triangles on its legs a and b, minus the area of the equilateral triangle on its hypotenuse, c. (W. Roberts, 2003, p.122)

A look-and-see proof

Note: all triangles which appear equilateral are equilateral.

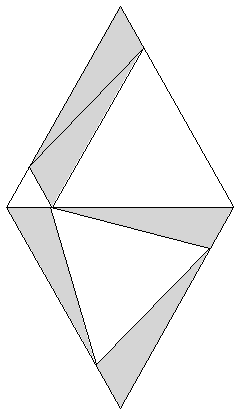
Eutrigon theorem, visual proof through resonant scale structure

Figure ET2

Detailing the proof (see figure ET3)

From Figure ET3 it can be seen that:

1) Triangles marked "Q" are congruent eutrigons since each contains one 60° angle, and their respective sides are equal.

2) Triangles A, B, and C are equilateral

3) A and B are the equilateral triangles on the legs of eutrigon Q, and C is the equilateral triangle on its hypotenuse. >

4) The overall diamond shape is a rhombus consisting of an upper and lower equilateral triangle of identical area.

5) Point "4" means that, expressed in terms of areas,
A + B + 2Q = C + 3Q,
and thus, Q = A + B - C

therefore the Eutrigon Theorem is proved.

Eutrigon Theorem, resonant scale structure with labels

Figure ET3

Now, some readers may not be satisfied that in the 'look & see' proof given above, that eutrigon Q may be any eutrigon . Before we prove this more rigorously let us imagine whether it is so.

Imagine an animation of equilateral-triangle C rotating while maintaining its equilateral shape but varying in size such that its vertices 'slide along' the outer equilateral triangle it is touching...[I've provided such an animated version below and added some colour to jazz it up a bit! It auto-loops a few times with a pause in between. If it has already been through its routine by the time you get to this part of the page, just click the 'refresh button' in your browser window, and it will start over.]

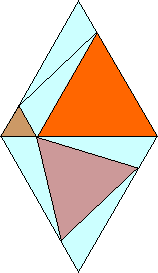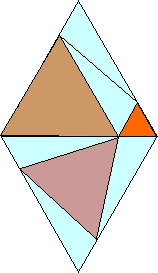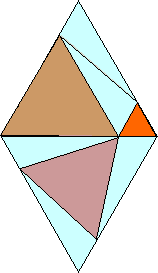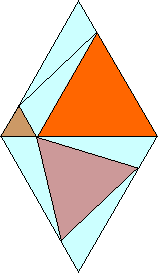
Eutrigon theorem, animated GIF version