Origins of the concept of the shape of number
- Early experimentations, and the shape-classification of number by the Pythagoreans
- (a) Nodes (common vertices of two or more adjoining shapes), shared edges (gapless 'symphyses'), and interstices (the form and shape of gaps) in geometric grids and tessellations
(b) implications of point (a) to the origins of the concept of square numbers and an interesting synchronicity between 'numbers of node points' and 'numbers of enclosed self-similar shapes' in the case of square configurations. - Scale structure theory applied to the so-called square numbers
- Implications of the scale structure of the plane to the consideration and classification of numbers as possessing the property of shape
- A new extended geometric understanding of the so-called square numbers (those of form p x p) and a fundamental scale structure in number theory
1
Towards a spatial understanding of numberThe emerging connections between number and geometry (viz. the Pythagorean Theorem ) pointed to new dimensions and to spatial properties of number that would transcend both their cardinal and ordinal aspects, upsetting the already now-settled (or so it seemed) measured linearity and regularity of the number line (fig. 5).
Figure 5 New properties of numbers seemed to relate to areas and geometric shapes as much as they did to lengths and quantities. Some numbers could be arranged into regular triangular lattices of dots, and hence were known as triangular numbers (fig. 6).
Figure 6. The ‘triangular numbers’ from 3 to 28 Similarly, other numbers could be arranged into square grids of dots and were thus named ‘square numbers’ (fig. 7).
Figure 7 The ‘square numbers’ from 4 to 36 The tetraktys To the Pythagoreans, the triangular number 10 was held in the highest esteem, and considered of supreme mystical significance. Its name, the tetraktys, meant literally ‘…“the holy fourfoldness”, representing the four elements: fire, water, air, and earth.’ (J. Gullberg, 1997, p. 289)
Figure 10 Wells observes that, gradually, the Pythagoreans described many other types of tetraktys or fourfoldness . ‘Magnitude , for example, comprised point, line, surface and solid.’(D.Wells, 1997, p.62) [See also fig. 4] |
|
2 Nodestone
The nodes (or geometric arrangements of 'stones') appear to have dominated the view of the early pioneers of number rather than the intervening shapes and spaces they mapped out. Thus these 'lodestones' appear to have captured the attention of the pioneers of number [over and above the empty (null) intervening spaces, replete not only with resonances of the concept of number, but of the zero too], and so the node-points of regular geometric configurations won the day in determining the provisional shape-classifications of numbers.
The stones themselves took precedence over and above the intervening shapes in the reckoning and classification of numbers. This geometric exploration and classification of numbers as square, triangular, pentagonal, ... was extremely far-sighted considering the time in which these early protagonists of number lived. Yet, as so often happens in history, 'provisional groupings' and 'provisional scale structures' gradually became institutionalised and accepted as 'facts', largely unquestioned for hundreds, if not thousands of, years.
'Square numbers' were now defined. In other words, fixed. Their geometry became powerfully bound to the very word 'square' and all that the word conjured up. Like many definitions, it attempted to reflect what was believed to be the geometrical nature of that special class of numbers whose factorization is symmetrical (p x p). But, in hindsight, this has turned out 'to hit upon only a single note' in what is in reality a fascinating 'scale of notes' (scale structure) that relate to these numbers. (The following web pages elaborate this point.)
The well-known idiom of speech, 'Thinking outside the square', thus not only paid an indirect homage to the dominance of the square within mathematics and (by implication) logic, and the difficulty of thinking outside its walls, but was also set to become one of the great ironies of mathematics itself —in mathematic's having decidedly thought within it for far too long.
Number nomenclature:
the origin of the name 'square number'
[This following section of the web page is quoted from my book (W. Roberts, 2003, pp.97—99) except for the interactive diagram appearing below as well as some adjustment to the text to accommodate this.]
Our persistence in using the square as the default unit-of-area in mathematics seems to be symptomatic of our square-sighted view of a special class of number whose very name, although indisputably logical in what it affirms, has blinkered our vision of their multifaceted symmetry. These special numbers are currently (and unfortunately) known simply as , 'the squares' .
 |
In the light of scale-structure theory, this name is not only 'square-sighted' but is short-sighted since as we shall see, these numbers are much more than simply square.
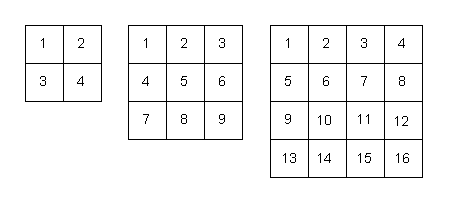
Perhaps a reason the polymorphic nature of these numbers was largely missed was that early exploration of the properties of numbers often involved the arrangement of pebbles into simple geometric shapes. The stones corresponded to the vertices or points of a geometric grid and these points also mapped out empty intervening geometric shapes. In the case of the square arrangement of stones, there is a curious synchronicity between the number of vertices (stones) and the number of intervening square spaces they map out (click buttons a and b in the diagram at left). 9 stones enclose 4 squares (as depicted in diagram), 16 stones enclose 9 squares, 25 stones enclose 16 squares, etc. The numbers are from the same set, and are 'in phase' but separated by one cycle. Thus no matter whether you counted the grid points or the intervening squares, you always got a number from the set {4, 9, 16, 25, ...} Whereas, a triangular grid yielded different numbers of stones (3, 6, 10, ...). Hence these latter were named 'triangular numbers'. It made perfect sense from that one point of view — the number of points or stones in the grid — but if you looked at the number of intervening empty triangular spaces mapped out by the triangular grid of stones, there was a surprising and beautiful connection. Namely, for any given side-length, the number of enclosed self-similar shapes was identical in both the square and triangular formats (refer to interactive diagram above, button b).
| The numerous symmetries of these amazing numbers (hitherto known as the squares) seems to have eluded many and remained largely unexplored, ignored, or of anecdotal interest for more than two thousand years. Very early in the history of mathematics, triangular numbers and square numbers became defined entities, distinct sets with distinct properties. The nomenclature was biased in favour of difference: 'How does this set differ from that set?' This emphasis on taxonomy (naming and cataloguing things) has affirmed connections at one level, but frequently at the expense of recognising (often more important) connections on other levels. This has also affected the arts. |
|
| back to top |
next > |


