Completing a scale structure of triangles:
Co-eutrigons and the Co-eutrigon theorem
This web page is reproduced from the author's book Principles of nature; towards a new visual language, WA Roberts P/L Canberra. 2003. [Used with permission of the author] edited and reformatted for the web, with some additional commentary for the sake of contextual clarity.
There exists a further double-resonance of the 120° angle in both the Cosine Rule (in which 2cosC= -1) and also in the scale structure of the three regular polygons that can tile the plane without gaps (one of these being the hexagon whose internal angles are 120°). These synchronicities suggest a third special class of triangle in which one internal angle equals 120°, and for which class we are justified in expecting a similar associated Pythagoras-like theorem (in light of scale-structure theory as discussed thus far).
Introducing another new class of triangle (as fundamental as the right triangle) and its associated theorem*
Let us thus define a triangle in which one angle equals 120-degrees to be a co-eutrigon (the prefix “co” signifying complement of the eutrigon).
Definition of a co-eutrigon
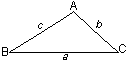
Let 
ABC be any co-eutrigon. We define angle C to be the 120° angle, a and b to be the ‘legs’ or sides adjacent to angle C , and c to be the hypotenuse or side opposite angle C.
Let a co-eutrigon be a triangle with one 120° internal angle.
The Co-eutrigon theorem
Introduction
This, and the Eutrigon Theorem (geometric form..), may be new. The closest theorem I have found to the geometric forms of the Eutrigon Theorem ... and the Co-eutrigon Theorem ... is the Napoleon Theorem.... Via a scale-structure approach including a consideration of the geometry in terms of relative units of area, I was able to deduce algebraic forms of the Eutrigon and Co-eutrigon Theorems. The resultant equations ( ab = a2 + b2 – c2 for eutrigons, and ab = c2 – a2 – b2 for co-eutrigons) were confirmed by, and geometrically reinterpreted, the Cosine Rule (in terms of relative units) when angle C = 60° and 120° respectively.
The Co-eutrigon theorem:
geometric form
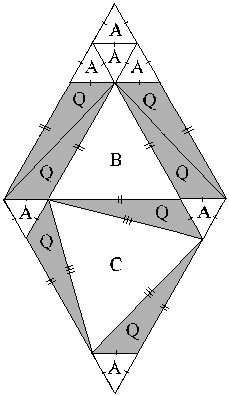
The area of any co-eutrigon [shaded in the diagram below] is equal to the area of the equilateral triangle on the hypotenuse c minus the sum of the areas of the equilateral triangles on legs a and b.
above, Figure C-ET1
A 'look-and-see' proof:
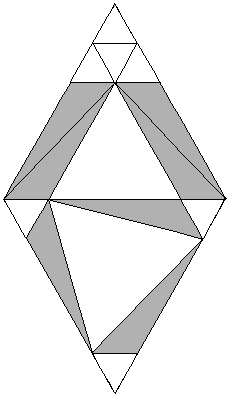
Figure C-ET2
Figure C-ET2 shows a resonant scale structure
which visually proves the Co-eutrigon Theorem.
Detailing the Co-eutrigon theorem proof
|
Figure C-ET3 |
Can Q be any co-eutrigon?
For reasons similar to those given in the case of the Eutrigon theorem, Q,...can represent any co-eutrigon, proving the theorem true for all co-eutrigons. We may summarise this reasoning as follows:
The shape of any co-eutrigon is specified by the ratio of its leg lengths, a/b. If we let the shorter of a eutrigon's legs be a, then the ratio a/b is always in the range 0 < a/b < (or equal to) 1. It can be seen from an examination of [the] figure ... that every ratio of a/b is possible in the diagram: a can be vanishing small or can be any value up to and including a = b. Thus every possible shape of co-eutrigon can be accommodated in the diagram without altering the geometric relations, and thus the theorem holds true for all co-eutrigons.
Co-eutrigon Theorem: algebraic form
The geometric form of the Co-eutrigon theorem states: the area of any co-eutrigon (i.e. a triangle in which one angle is 120°) is equal to the area of the equilateral triangle on its hypotenuse ‘c’ minus the combined areas of the equilateral triangles on legs ‘a’ and ‘b’ [see figure C-ET1 above]. How can this be expressed algebraically, that is, as an equation?
Earlier we determined the area of an equilateral triangle in etu (which is simply p2 where p is the side length) but we have not yet determined the equation for the area of a co-eutrigon in etu. However, there is a beautiful synchronicity with the equation for the eutrigon’s area which follows from a correspondence of the triangle altitudes between eutrigons and co-eutrigons. This again reflects the complementary relationship between the two classes of triangle.
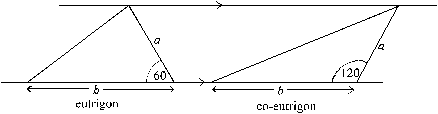
It is well-known and easily proven that triangles of the same base and same altitude have the same area. This means that there is a surprising resonance between a eutrigon’s and co-eutrigon’s areas —if legs a and b (i.e. the sides adjacent to the defining angle) are equal then it follows that they have the same area, namely their product, ab (as expressed in etu), [see figure below].
These two triangles have the same area because their bases and altitudes are the same.
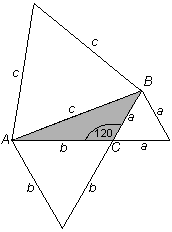
We may demonstrate the complementarity of these triangles more clearly by placing them as [below],
Same triangles as above but here placed side-by-side to highlight their complementarity. The area of each triangle is identical when the bases b are equal and share the same 60° altitude a.
So the area of a co-eutrigon expressed in etu is the same as for the corresponding eutrigon of the same respective leg lengths and thus simply the product of the co-eutrigon’s leg lengths, ab.
We can therefore state the algebraic form of the Co-eutrigon Theorem in terms of the new relative units of area (etu) as,
The area of a co-eutrigon (given in etu) = ab = c2 – a2 – b2
This follows from [Figure C-ET3] and the ‘area equation’, Q = C – A – B.
As with the Eutrigon theorem’s algebraic form discussed earlier, the Co-eutrigon Theorem is also consistent with the Cosine Rule and is the same as that rule for the special case when angle C = 120°. ... Since 2CosC = -1, the Cosine Rule reduces to c2 = a2 + b2 + ab and, rearranging terms, we obtain the Co-eutrigon theorem form above,
ab = c2 – a2 – b2
Including the Pythagorean equation, we now have three Pythagoras-like equations and their corresponding geometric theorems (through the induction of relative units). Given that a and b are the sides adjacent to the defining angle (e.g. the 90° angle of a right triangle), and c is the hypotenuse or side opposite the defining angle, the three equations are:
- a2 + b2 = c 2 . . . . Pythagoras’ Theorem for case when C = 90°
- ab = a2 + b2 – c2 . . . . . . Eutrigon Theorem; C = 60°
- ab = c2 – a2 – b2 . . . . . . Co-eutrigon theorem; angle C = 120 E
These three equations and their associated geometric forms exactly correspond (via their respective stipulated internal angle) to the three regular polygons (equilateral triangle, square, and hexagon) which can uniformly tile the flat plane without gaps.
This then completes a scale structure of not only three algebraic theorems but of their corresponding resonant geometric theorems, and it is reasonable to conjecture, I feel, that when recognised and implemented as a complete scale structure within mathematical practice, and utilised in ‘resonant application’, that significant advances may follow in number theory and in our understanding of the foundations needed for a new visual language and music.
For example, the whole sub-discipline of trigonometry may now be re-examined in light of the new geometric understanding of the above equations (which includes the critical notion of relative units).
Number theory too is likely to be extended via the key of the relative unit, and will call into question the very foundations of number and the meaning of ‘integers’—of how they are written or represented, and of new operations, properties, and transformations that may now be discovered and made possible.
| back to top |
next > |