Scale structure theory applied to square numbers

Principles of Nature: towards a new visual language

Scale structure theory applied to the square numbers

This web page is quoted from the author's book Principles of nature; towards a new visual language, WA Roberts P/L Canberra. 2003. [Used with permission of the author] - minor editing for the web

In the regular division of the plane, there exists a scale structure of only three distinct regular polygons which can tile the plane to infinity in every direction without gaps. They are the square, the equilateral triangle and the hexagon.

The three regular polygons which can tile the plane without gaps

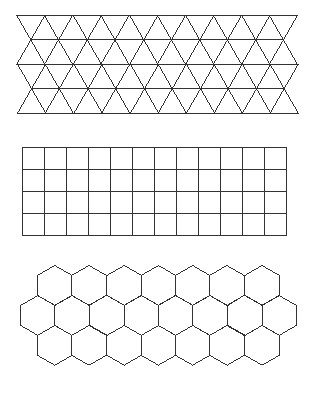
These gapless tiling patterns (known as tessellations of the plane) are demonstrated in the next figure (Figure 6.7)

Figure 6.7
There are only three regular polygons whose sides and angles are equal and which can tile the plane without gaps: the square, the equilateral triangle, and the hexagon

That only these three regular polygons can tile the plane without gaps and in self-similar manner is a fact that has been known by geometers for centuries and is easily proven (Dunham, 1994, pp. 108-111). What is perhaps not recognised or undervalued is the potential significance of such a fact. [This appears to be symptomatic of a problem in current cultural attitudes to knowledge and research, and will be briefly addressed later.]

We should therefore expect that these three shapes contain within themselves and within this triadic scale, important clues to the structure and form of the infinity which they divide. Just as the time it takes for an echo to return reflects the distance of a rock face on the other side of a gorge, so these shapes ought to reflect something about the nature of the infinity they divide. And because they divide this infinity in a self-similar way, that is, because they divide this infinity into integral units, we expect these shapes will reflect something important about the whole-numbers themselves. More particularly, they should reflect something important about special sorts of whole number, because, of all the regular polygons (i.e. having equal side-lengths and internal angles), there are just three which can tile the plane without gaps. Since polygons are shapes which occupy area, and since areas can be expressed numerically in a multiplicative manner (length x breadth), we should expect numbers of a symmetrical composition in the form p x p (that is, p²) may be connected to these particular regular polygons in certain special ways. That is exactly what we find. These special sorts of whole number we currently know as the squares.


Since polygons are shapes which occupy area, and since areas can be expressed numerically in a multiplicative manner (length x breadth), we should expect numbers of a symmetrical composition in the form p x p (that is, p²) may be connected to these particular regular polygons in certain special ways. That is exactly what we find. These special sorts of whole number we currently know as the squares.

The line of reasoning may be schematically summarised as in figure 6.7 below.

Figure 6.7
Line of reasoning leading to the scale structure of the plane

The square property of numbers of the form p² has been widely known for more than two thousand years. But on the preceding page (click button b ) we have seen a less familiar triangular representation of the 'square number' 4. We need to show if this triangular characteristic is a property of just some of the square numbers, or all of them.

Do all square numbers have a corresponding triangular form?

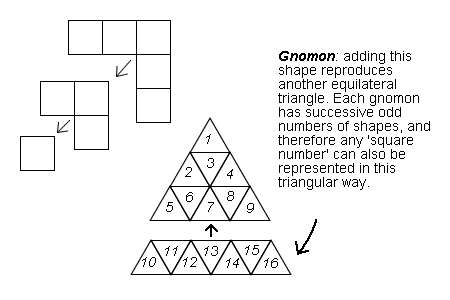
It has long been known that the squares can be generated by the successive addition of the members of the set of odd numbers (1+3=4, 1+3+5=9, 1+3+5+7=16, ...). Geometrically, these odd numbers may represent integral areas which are added to a given shape, and such added shapes were called gnomons by the Greeks if they could regenerate the original figure (see figure 6.8). Clearly, it can be seen that for each unitary increase in the side-length of either squares or equilateral triangles, the gnomon consists of successive odd numbers of component self-similar shapes. Each successive gnomon contains two more units than its predecessor. And therefore each successive gnomon includes successive members of the set of odd numbers and can therefore form successive numbers of the form p². Thus every square number can just as easily be represented in equilateral triangular form.

Figure 6.8 Illustrating gnomons which when added to a given shape reproduce the original

What about hexagons?

A significant oversight and omission is thus revealed at the fundamental level of the notion of the unit in mathematics—at the very least, units pertaining to the measurement of areas (also refer: Schrödinger's observation)— including the concept of units as taught in primary, secondary, and even (sometimes) tertiary education

[In light of the equally-triangular nature of the so-called 'square numbers'] ..is it not curious then, that in the history of mathematics, squares have served the role of 'general-purpose units-of-area', it would appear by default rather than design*? We have applied square plugs to nearly every shaped hole under the mathematical sun. The notion of units-relative-to-wholes has not been taken up seriously perhaps because issues of comparison have tended to focus on differences more than similarities or 'resonances'. In the comparative measurement of areas, we have inducted the square as the default unit of area and a universal arbiter of comparison ('this area is so-many-square units whereas that area is a lesser number of equivalent square units, and is therefore smaller'). It is ironic because comparisons involve relating something to something else, and thus a choice of units relative to the system concerned must ultimately be simpler and more powerful.


We have applied ‘square plugs’ to nearly every shaped hole under the mathematical sun.

As will be shown in the following pages, the application of relative units to mathematical and spatial problems allows a deeper understanding of qualitative differences as well as a simpler and more resonant connection of geometric problems to number theory and analysis.

^ 1.8 mb Flash video. [When you see a picture of the author in the square above, then the video is ready to play. Please press the triangular play button (lower right corner of above square) that will also be visible when the movie is ready.] The movie contains further observations by the author on the concepts of units and of integers and for the need of a major rethink surrounding the nature of the wholeness of a number or unit. What makes something whole? Has the number-line model limited our vision of the wholeness of numbers? Can numbers be shapes? And need the shape of a number be unique or might it be a shared property among numbers? Could there remain syntaxes to be discovered which govern these interconnections and the new 'properties' of number when viewed as higher-dimensional 'wholes'? What does the new theory say on the question of the 'primeness' of numbers, and do these questions in turn challenge the validity, or at least the significance, of the Fundamental Theorem of Arithmetic.