Appendix 1
Semi regular tessellations of the plane
The following are well-known and there are only these eight as shown below (in addition to the three regular tessellations by equilateral triangles, squares, and hexagons) which satisfy the criterion that each intersection-point (node) is surrounded by regular polygons in exactly the same way. The definition however is curious in that the congruence is from the perspective of the points-of-intersection of the grid rather than of side-lengths or of shapes. This rings some alarm bells in that it reminds us of how the early number theorists seemed to have counted the stones which formed the apices (or ‘nodes’) of their geometric lattices but, in the excitement of the emerging patterns, perhaps forgot about the intervening spaces their stones had mapped out, and therefore numbers of the form p2 became known as simply ‘the squares’.
The aforementioned point (no pun intended) is very interesting and means we must bear in mind that we are considering a ‘regularity of’ or identity in ‘the perspective from a node-point of the grid’.
So then, if you look for a congruence of the points-of-intersection in tessellations with regular polygons, then you allow for these extra tessellations (as shown below) in which each tiling is achieved by means of more than one type of regular polygon. Curiously, the notion of tessellations or ‘tilings without gaps’ is brought into question, since (especially with the two-shape tilings) one shape may be viewed as the ground of the other—in other words, as ‘gaps’ between the others. It works the other way around too (following a Gestalt shift in perception) such that the figure-ground arrangement is reversed—what was the ‘gap’ now becomes the ‘figure’. Notice then, how words (e.g. “gaps”, “square numbers”) are active in how we perceive the world.
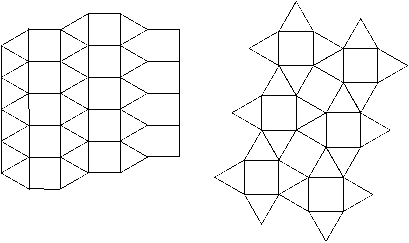

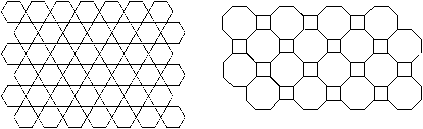
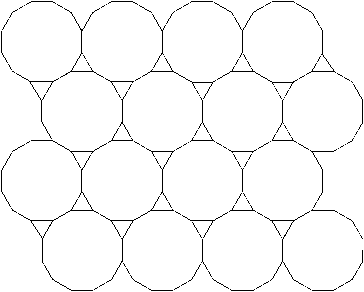
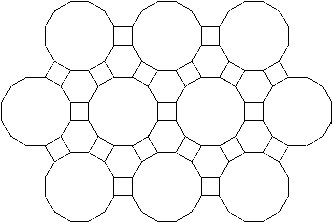
Two tessellations of the plane with two regular polygons: squares and equilateral triangles (1 & 2),
hexagons and equilateral triangles,
hexagons and equilateral triangles2,
hexagons and squares
equilateral triangles and dodecagons
squares, hexagons and dodecagons.
equilateral triangles, squares and hexagons.