Triads in music and math
Just as Euclid's famous treatise, The Elements, began with the figure of an equilateral triangle, I can find no better figure from which to start (see the section, An application of scale structure theory to number and geometry) in order to re-examine the origins and history of mathematics and geometry. And from there, to consider the plausibility of alternative more powerful numerical notations than the current method of representing numbers allows, proceeding via an awareness of the principle of Universal interconnectedness, to strive towards that summit—an understanding of the signs and syntax of a new visual language combining both art and science within the dynamics of a 'new naturalism'. This will be increasingly understood in the future by virtue of the unquestionable existence of a Universal yet covert network of synchronicities, resonances, conjugations and 'logical conjunctions' which, acting in concert, lead towards 'stable states' (scale structures) in both morphology and natural phenomenology. At present, such a visual extension to the language of music, indeed of a new kind of aesthetic logic itself (and the powers it will undoubtedly open up), stands monumentally statuesque before us like a new Mount Everest.
Thus we start with a fundamental principle of harmony (and also therefore of resonant scale structures)— the triangle-related concept of the triad in both music and math.
Triads in music
Triads in music simply consist of three notes sounding together at the same time. Some may better know these as 'chords' (of which they are really a subset).
Change among the relative intervals within a chord or scale bestows upon it an 'identity' and 'character' that the brain can recognise, and moreover, often evokes an emotional response. It is quite amazing just how subtle a change can be (for example, affecting just one of the three notes of a triad) and yet still effect a pronounced 'altered emotional state' in our perception of the whole triad as 'bright and happy' (usually associated with major triads and scales) or 'sad and melancholy' (termed minor triads and scales). [Play the animation below to hear the difference between a major and minor chord. Ask yourself which one sounds bright and cheery and which one sounds a little more introspective and melancholy? The neurophysiological question of 'why?' remains insufficiently answered (in my view).]
It is fascinating how the single consistent difference between the so-called major and minor triads or scales is a change affecting the third note of the diatonic scale. This fact in itself is, one senses, no random 'fluke' of nature and once again underlines a fundamental significance in Nature of the number 'three' (which the Pythagoreans considered to be the first 'number'), the 'third' (as in music), and of course, triangles and their relations (such as triads). Altering the third note of the 8-note diatonic scale downwards by just one semitone bestows upon the whole scale a sense of melancholy, mournfulness, yearning, (and the associated human emotions of the 'minor keys' of music), and this remains an unexplained mystery of music and the human experience of it.
Pythagorean triads
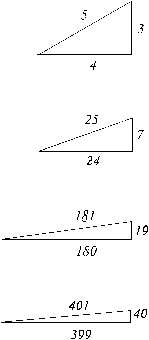Pythagoras' Theorem is almost certainly the most widely-known and applied theorem in mathematics today. We shall look at it a little more closely later in this web document, but here we shall restrict ourselves to what are known in mathematics as Pythagorean Triads (or triples)—three whole numbers which can together form the sides a right triangle (one in which one angle is equal to 90 degrees).
Note that there are many more right triangles in which at least one side is not an integral (whole-number) length, so this special subset of right triangles (in which every side is an integral length) is a very interesting class of right-angle triangles and fascinated the Pythagoreans who had coincidentally discovered the connection between whole-number ratios and pleasing 'harmonious' intervals of sound which formed the basis of music. No wonder then that they explored these triads in greater depth. In fact, they were able to derive three special equations (known as parametric equations) that could generate, at whim, a myriad of these Pythagorean triads (three whole numbers) which when joined end-to-end formed the sides of a right triangle.
I agree with historians who consider that this discovery and these equations (which connected the geometric form of the Pythagorean theorem to the numerical equivalent via their elucidation of the patterns behind the Pythagorean Triads) represented a key breakthrough that was to quickly become a 'world-view changing moment' and which led the Pythagoreans to their famous inference concerning the entire cosmos— that 'all is number'. It was a thoroughly abstract idea, distilled and profound, that stands very near to the origins and concept of logic itself, and 'proof' as a method of extending knowledge in a connected abstract form yet which seems to miraculously parallel the physical nature and motion of the Universe itself in a most compelling and inspiring way*.
 |
|
| Numbers, as originally conceived, were the pragmatic progeny of accounting and commerce; but slowly, as they ‘grew’, were seen by the Pythagoreans (and others) as having a meaning that stretched far beyond the mere representation of ‘quantities’ and the collections of material objects that had spawned their introduction. |
|
|
|
| back to top |
next > |