The area of an equilateral triangle in etu
This web page is quoted from the author's book Principles of nature; towards a new visual language, WA Roberts P/L Canberra. 2003. [Used with permission of the author]
We have established in our discussion of so-called 'square numbers' that p2 numbers are profoundly connected to equilateral triangles and not just squares. We can put our finding this way: equilateral triangles can be dissected into p2 numbers-of-smaller-equilateral-triangular-units. And we can therefore express an equilateral triangle's area as being equal to p2 etu, in other words, that the number of etu's which fills its area without gaps is equal to p2, where p is the number of etu side-lengths which fit along a side of the equilateral triangle in question. In equation form,
The area of an equilateral triangle of side-length p (expressed in etu) =p2
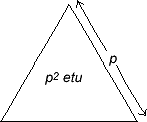
The equilateral triangle has a side-length p-times as large as the smaller equilateral triangular unit of area (or ‘etu’), and its area is p2 as large...
Notice the simplicity and symmetry of such a relationship. The beautifully simple relationship given above is muddied if we try to understand equilateral triangular areas and side-lengths in terms of squares (which is what we have done for more than two thousand years).
To remind us of this, let us compare and contrast our traditional 'square' handling of equilateral triangular areas [see diagram below]. What is the area of an equilateral triangle of unitary side-length expressed in square units? [This is easy for any high-school student but is not as easy as finding the area in etu which is simply p2 as given above!]
 |
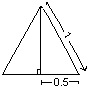Illustrating the traditional method of calculating the area of the most symmetrical and fundamental triangle: that of an equilateral triangle of unitary side-length, according to an application of Pythagoras' Theorem |
The area of any triangle in square units is 2 bh where b is the base-length and h the perpendicular height of the apex from the base. We can find h by Pythagoras' theorem ... which equals 
3/2. The area (½bh) is therefore equal to 
3/4 square units. This irrational number results from applying a square peg to a triangular hole (see figure on this page). The fit is awkward, complex, and dysfunctional. [See diagram below]
 |
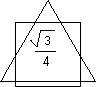Such a calculation, based upon square units of area, returns an irrational number, since it results from 'applying a square plug to a triangular hole'. |
| back to top |
next > |